Table des annales

 

EXERCICE I :

1) On calcule :

Comme P est inversible, elle correspond à un produit de matrices élémentaires, donc B est ligne-équivalente à A. On note : B~A.

 

 

2) a) En appliquant successivement les opérations élémentaires suivantes : L₃(-1/3), L₁₃(-1) puis L₂₃(1), on trouve R la l.r.e. de B (donc de A vu que B~A)

 

     b) R possède trois colonnes pivots donc rang(R)=3.

 

3) D’après le Théorème 4 (3^e propriété), on a, par lecture directe de R, toutes les combinaisons linéaires (non redondantes !) entre colonnes de R
(donc de A vu A~R). Les voici (avec Aⁱ la i-ième colonne de A) :

A³=3A¹+2A² ; A⁴=A¹+A² ; A⁶=2A¹+A²+A⁵ ; A⁷ = 2A¹+A²-A⁵

 

4) P est inversible car on a trouvé une matrice R, l.r.e., telle que A~R. Cela signifie que P correspond à une suite d’opérations élémentaires, donc est un produit de matrices élémentaires, et par conséquent est inversible. Nul besoin de calculer P^-1.

 

EXERCICE II :

1)  I E  car I = M_(1,0,0) B E  car B = M_(0,1,0) et C E  car C = M_(0,0,1).

2)  B n’est pas inversible car contient 2 lignes identiques, donc est de rang < 3.

C est inversible car est une matice élémentaire correspondant à l’opération élémentaire L₁₃.
3) a)  ;  ; .

     b)  ;  ;  ;  

     c)  E car  = M_(1,0,1). De plus, ,  et  sont aussi des matrices de E  car on a prouvé (question 1) que I  et B sont des matrices de E.

4) αI+βB+γC=0  
 α=β=γ=0)

 

5) Le même calcul que ci-dessus avec a, b, c à la place de α, β, γ δ donne bien :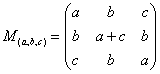

On en déduit que «toute matrice M_(a,b,c) de E s’écrit comme combinaison linéaire de I, B et C.

 

6) Soient  et  deux matrices de E . Montrons que M₁+M₂ est aussi une matrice de E . Or , CQFD.

7) Avec les mêmes notations, Formons le produit M₁M₂ et montrons qu’il appartient à E. Après calcul du produit, utilisation des 4 formules de la question 3b, et factorisation, nous obtenons :

 donc  qui est bien une matrice de E.

8) On considère la matrice  

     a)  ;  ;  

     b) Si n pair : . Si n impair :  

9)

     a)  

     b) I et 2A commutent, donc on peut leur appliquer la formule du binôme de Newton : 

nN*,   en utilisant 8b)

 

     c)  

     d) Formule du binôme :  

                    On en déduit :   

   De même :  

                    On en déduit :   

     e)  

10) En repartant de 9c), on obtient finalement :

 

 

 

EXERCICE I :

·       P est une matrice triangulaire inférieur, donc elle est inversible et son inverse est la matrice triangulaire supérieur qui lui est symétrique.

·       P est inversible mais n’admet qu’un inverse à gauche car elle possède une diagonale nulle à droite.

·       Pour justifier que P est réversible il faut multiplier la matrice P par la matrice identité. Or PI=P donc P est réversible.

EXERCICE II :

·       I, B, C sont des matrices de E car si on remplace a, b et c par les valeurs de I, B et C, elles vérifient toutes les 3 l’ensemble des matrices M(a,b,c) désigné par E.

·       B et C sont des matrices carrées, elles sont donc a priori inversibles.

·       L’inverse de B est la matrice Identité I

·       1+2ⁿ=3ⁿ

·       Pour B, on remarque (intuitivement) qu’il est très facile de calculer sa LRE, elle est donc inversible.

·       B et C sont inversibles car BC=CB

·       D=I+1/A

·       B = (1 0 3 1 1 3 1) c’est donc la ligne réduite échelonnée de A.