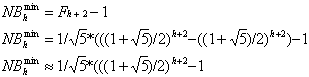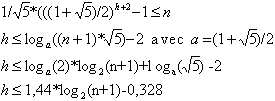précédent | suivant | table des matières
|
|
L'efficacité des algorithmes précédents dépend considérablement de la forme de l'arbre sur lequel on travaille : la situation la pire est celle d'un arbre binaire ordonné dont chaque noeud n'a qu'un seul successeur droit ou gauche : l'arbre se comporte alors comme une liste et les algorithmes précédents ont une complexité temporelle de l'ordre de n, nombre de noeuds de l'arbre. Les algorithmes précédents auront une complexité de l'ordre de log2(n) si l'arbre est dit équilibré, c'est le meilleur des cas.
En moyenne en revanche, nous venons de démontrer dans le paragraphe précédent que les algorithmes de recherche, d'ajout et de suppression ont un coût moyen de l'ordre de oge(n). Ce qui est intéressant c'est de calculer le rapport coût moyen sur coût optimum. Nous avons :
2*loge(n)/log2(n) = 2*loge(2) = 1,386
Il faudra faire très attention à ce nombre avant de se lancer dans des opérations de rééquilibrage ; il faut que le coût supplémentaire entraîné par le rééquilibrage ne soit pas supérieur au bénéfice escompté par le rééquilibrage, sauf éventuellement si le nombre de recherches est de beaucoup supérieur au nombre des ajouts ou des suppressions qui engendrent des rééquilibrages.
Cependant, dans de nombreuses applications, la séquence des insertions n'est pas aléatoire : il faut alors se poser le problème de faire en sorte que l'arbre ne dégénère pas en une liste, de façon à conserver aux algorithmes toute leur rapidité.
1 Définition.
Un arbre binaire équilibré, ou arbre AVL (du nom des auteurs de la méthode : Adelson, Velskij, et Landis ) est un arbre binaire tel que les hauteurs des deux sous-arbres de tout noeud de l'arbre diffèrent de 1 au plus :
|h(Ag) - h(Ad)|≤1
Ceci entraîne évidemment la propriété que tout sous-arbre d'un arbre binaire équilibré au sens AVL est un arbre équilibré au sens AVL.
1.1 Evaluation préliminaire.
Avant d'étudier les
algorithmes qui permettent de maintenir un arbre binaire
équilibré au sens AVL,
il est nécessaire de s'assurer que le gain sera
intéressant.
La question est de
savoir quelle est la hauteur maximale que peut avoir un arbre binaire
équilibré
au sens AVL. Pour cela nous allons nous occuper de la question inverse, à
savoir quel est le nombre minimal de noeuds que peut avoir un arbre binaire
équilibré au sens AVL de hauteur h.
Nous avons :
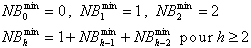
Cette récurrence a pour solution le nombre de Fibonacci au rang h+2 moins 1. Soit :
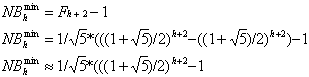
Donc réciproquement la hauteur maximale h d'un arbre AVL contenant n éléments est telle que :
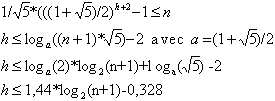
La complexité en pire cas
des arbres binaires éqilibrés au
sens AVL est donc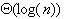 
.
2 Algorithmes de rééquilibrage.
A chaque noeud de l'arbre, nous ajoutons une information indiquant quel est le sous-arbre le plus haut :
class NoeudAVL{
private Comparable element;
private NoeudAVL gauche, droit;
private int equilibre;
public NoeudAVL(){
gauche = null;
droit = null
equilibre = 0;
}
public NoeudAVL(Comparable e, NoeudAVL g, NoeudAVL d){
element = e;
gauche = g;
droit = d;
equilibre = 0;
}
}
La classe ArbreAVL est définie comme suit :
class ArbreAVL{
private NoeudAVL racine;
private boolean equilibreD ( NoeudAVL r, NoeudAVL p, boolean g){
...
}
private boolean equilibreG ( NoeudAVL r, NoeudAVL p, boolean g){
...
}
public void ajout(Comparable o){ ... }
}
Supposons que le noeud A était précédemment équilibré :
Lors d'une insertion dans le sous-arbre gauche deux cas se présentent :
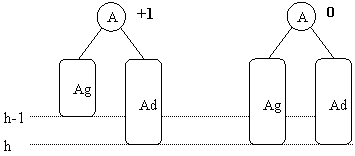
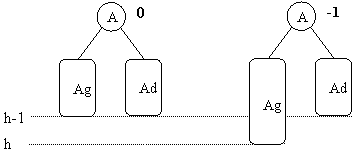
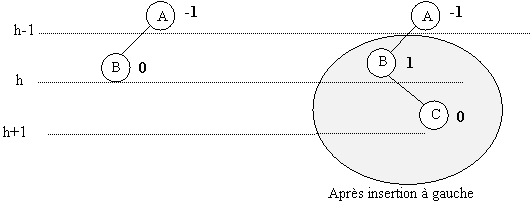
Les deux cas où l'arbre reste équilibré bien que la hauteur du sous-arbre gauche augmente sont les suivants :
 |
 |
Dans le premier cas la hauteur de l'arbre n'augmente pas, alors que dans le second cas elle augmente.
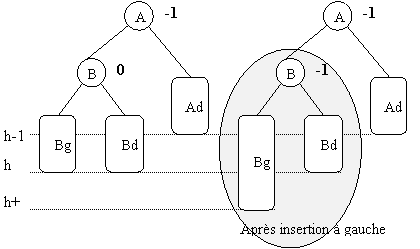
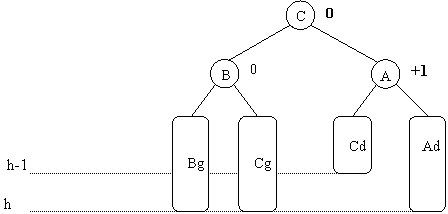
Etudions les différentes possibilité qui se présentent lorsque l'arbre est déséquilibré. Supposons qu'avant l'insertion la hauteur du sous-arbre droit soit h-1, la hauteur du sous-arbre gauche avant l'insertion était égale à h, elle a augmenté lors de l'insertion, et est donc maintenant de h+1. Soit B le sous-arbre gauche de A. Deux possibilités se présentent :
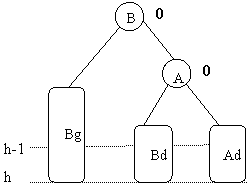
B penche gauche.
 |
Devient après ré-équilibrage :
 |
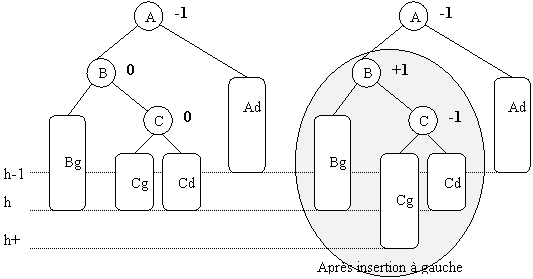
2) B penche droite.
Deux possibilités :
|
 |
Ou un au moins des deux arbres Cg ou Cd a une hauteurh+1, l'autre pouvant avoir une hauteur h,
et c'est celui sur lequel se produit le déséquilibre.
Cet arbre devient après ré-équilibrage :
 |
Nous appellerons rotation chacune de ces opérations. Il est à remarquer que la deuxième rotation peut être obtenue en répétant deux fois la première rotation.
La méthode de rééquilibrage suivante est appelée après un ajout dans le sous-arbre droit qui a provoqué une augmentation de la hauteur du sous arbre droit :
boolean equilibreD ( NoeudAVL r, NoeudAVL p, boolean g){
// r est le fils gauche de p si g vaut true, r est le fils droit de p si g vaut false
// retourne true si après équilibrage l'arbre a grandi
NoeudAVL r1, r2;
switch(r.equilibre){
case -1 : r.equilibre = 0; return false;
case 0 : r.equilibre = 1; return true;
case 1 :
default : r1 = r.droit;
if(r1.equilibre == 1){
r.droit = r1.gauche; r1.gauche = r;
r.equilibre = 0;
r = r1 ;
}else{
r2 = r1.gauche; r1.gauche = r2.droit;
r2.droit = r1;
r.droit = r2.gauche; r2.gauche = r;
if(r2.equilibre == 1) r.equilibre = -1;
else r.equilibre = 0;
if(r2.equilibre == -1) r1.equilibre = 1;
else r1.equilibre = 0;
r = r2;
}
// refaire le chaînage avec le père
if(p==null) racine = r;
else if( g ) p.gauche = r ;
else p.droit = r ;
r.equilibre = 0;
return false;
}
}
La méthode de rééquilibrage suivante est appelée après un ajout dans le sous-arbre gauche qui a provoqué une augmentation de la hauteur du sous arbre gauche :
boolean equilibreG (NoeudAVL r, NoeudAVL p, boolean g){
// r est le fils gauche de p si g vaut true, r est le fils droit de p si g vaut false
// retourne true si après équilibrage l'arbre a grandi
NoeudAVL r1, r2;
switch (r.equilibre){
case 1 : r.equilibre=0; return false;
case 0 : r.equilibre = -1; return true;
case -1 :
default : r1 = r.gauche;
if(r1.equilibre==-1){
r.gauche = r1.droit; r1.droi t= r;
r.equilibre = 0; r = r1;
}else{
r2 = r1.droit; r1.droit = r2.gauche; r2.gauche=r1;
r.gauche=r2.droit; r2.droit = r;
if(r2.equilibre == -1) r.equilibre = 1;
else r.equilibre = 0;
if(r2.equilibre == 1) r1.equilibre =-1;
else r1.equilibre = 0;
r=r2;
}
// refaire le chaînage avec le père
if (p == null) racine = r;
else if( g ) p.gauche = r ;
else p.droit = r ;
r.equilibre = 0;
return false;
}
}
2.1 Ajout.
La fonction d'ajout est écrite alors de la façon suivante :
void ajouter ( Comparable x){
ajoutAVL( racine, null, true, x);
}
boolean ajoutAVL(NoeudAVL r, NoeudAVL p, boolean g, Comparable e){
if(r == null) {
r = new NoeudAVL(e, null, null);
if (p == null) racine = r
else if(g) p.gauche = r;
else p.droit = r;
return true;
}else{
int a = e.compareTo(r.element);
if (a==0) return false;// a déjà présent dans l'arbre
if (a<0)
if(ajoutAVL(r.gauche, r, true, e)) return equilibreG(r, p, g);
else return false;
else
if(ajoutAVL(r.droit, r, false, e)) return equilibreD(r, p, g);
else return false;
}
}
2.2 Suppression.
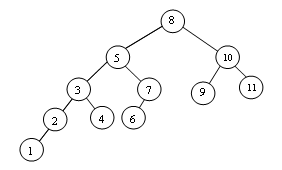
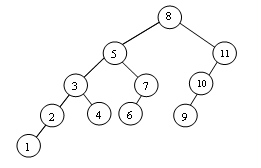
Une suppression peut entraîner plusieurs rotations pour le re-équilibrage de l'arbre :
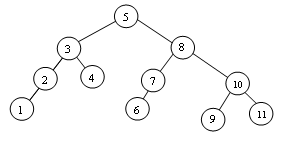
| l'arbre avant suppression de 12. | l'arbre après suppression de 12. |
|
|
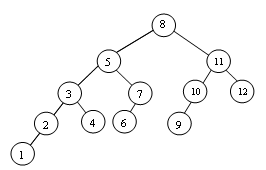
La suppression de 12 : entraîne les 2 rotations
|
|
boolean EquilibreDS ( NoeudAVL r, NoeudAVL p, boolean g){
// retourne true si la hauteur de l’arbre a diminué
// false sinon
NoeudAVL r1, r2 ;
switch (r.equilibre){
case -1 : r.equilibre = 0; return true; a
case 0 : r.equilibre = 1; return false;
case 1 :
default : boolean h; r1 = r.droit;
if(r1.equilibre==-1) {
r2 = r1.gauche; r1.gauche=r2.droit; r2.droit=r1;
r.droit=r2.gauche; r2.gauche = r;
if(r2.equilibre==1) r.equilibre = -1;
else r.equilibre = 0;p;
if(r2.equilibre==-1) r1.equilibre=1;
else r1.equilibre = 0;
r=r2; h = true; r.equilibre = 0;
}else{
r.droit=r1.gauche; r1.gauche=r;
if(r1.equilibre==0){
h = false;
r.equilibre=1; r1.equilibre=-1;
}else{
// entraîne une diminution de
// la hauteur de l’arbre
h = true;
r.equilibre=0; r1.equilibre=0;
}
r=r1;
}
if(p==null) racine = r;
else if( g ) p.gauche = r;
else p.droit = r;
return h;
}
}
boolean EquilibreGS ( NoeudAVL r, NoeudAVL p, boolean g){
// retourne true si la hauteur de l’arbre a diminué
// false sinon
NoeudAVL r1, r2 ;
switch (r.equilibre){
case 1 : r.equilibre = 0; return true;
case 0 : r.equilibre = -1; return false;
default : boolean h;
r1 = r.gauche;
if(r1.equilibre==1){
r2 = r1.droit; r1.droit=r2.gauche;
r2.gauche=r1; r.gauche=r2.droit;
r2.droit = r;
if(r2.equilibre ==-1) r.equilibre = 1;
else r.equilibre =0;
if(r2.equilibre == 1) r1.equilibre=-1;
else r1.equilibre=0;
r=r2;
r.equilibre = 0; h=true;
}else{
r.gauche=r1.droit;
r1.droit=r;
if(r1.equilibre==0){
h=false;
r.equilibre = -1; r1.equilibre = 1;
}else{
// entraîne une diminution de
// la hauteur de l’arbre
h=true;
r.equilibre = 0; r1.equilibre = 0;
}
r=r1;
if(p==null) racine = r;
else if( g ) p.gauche = r;
else p.droit = r;
return h;
}
}
La suppression est alors :
public void supprimer( Comparable x){
suppAVL(x, racine, null, true);
}
boolean suppAVL(Comparable e, NoeudAVL r, NoeudAVL p, boolean g){
// retourne true si la hauteur de l’arbre a diminué
if (r == null) return false;
else
if(r.element.compareTo(e)==0) return SuppAVL(r, p, g);
else if(e.compareTo(r.element)<0){
if(suppAVL(e, r.gauche, r, true)) return EquilibreDS(r, p, g);
else return false;
}else{
if(suppAVL(e, r.droit,r, false)) return EquilibreGS(r, p, g);
else return false;
}
}
boolean SuppAVL( NoeudAVL r, NoeudAVL p, boolean g){
// suppression effective du noeud r
// retourne true si la hauteur de l’arbre a diminué
NoeudAVL a, b;
a = r;
if(r.gauche==null) {
if( p==null) racine = r.droit;
else if( g ) p.gauche = r.droit;
else p.droit = r.droit;
return true;
}else
if (r.droit==null) {
if( p==null) racine = r.gauche;
else if( g ) p.gauche = r.gauche;
else p.droit = r.gauche;
return true;
}else{// les 2 sous arbres sont non vides
b = r.gauche;
while(b.droit!=null) b = b.droit;
r.element = b.element;
if( suppAVL(b.element, r.gauche, r, true)) return EquilibreDS(r, p, g);
else return false;
}
}
3 Evaluation.
On a vu que la hauteur d'un arbre binaire équilibré au sens AVL est inférieure à 1,44*log(n), de plus lors d'un ajout, il y a au maximum une rotation effectuée, donc l'ajout d'un élément dans un arbre AVL est en pire cas en (log(n)). Une suppression en revanche peut entraîner jusqu'à og(n) rotations, bien que les résultats expérimentaux montrent qu'en moyenne il n'y a qu'une rotation toutes les 5 suppressions. La suppression est donc en pire cas en (log(n)).
Les évaluations en moyenne des algorithmes sur les arbres binaires équilibrés au sens AVL sont des problèmes qui ne sont pas encore complètement résolus.