précédent | suivant | table des matières
Le nombre de comparaisons effectuées lors de la descente ou lors de la remontée d’un élément dans un tableau ayant n éléments, est au maximum égal à la hauteur de l’arbre binaire représenté par l’arbre. Un arbre binaire complet de n éléments a une hauteur de log2(n)+1
La fonction organiserTas définie par :
void organiserTasBis( int t []){
for(int i = t.length/2; i>=1; --i) descendre(t, i);
}
a une complexité linéaire. En effet :
Si n = 2m-1 la complexité est donc 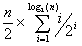
Calculons la récurrence : 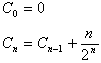
Posons 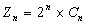 , nous avons alors la récurrence :
, nous avons alors la récurrence :
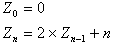 Nous pouvons démontrer par récurrence que
Nous pouvons démontrer par récurrence que 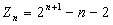
Ou le montrer directement :
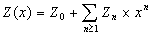
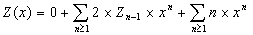
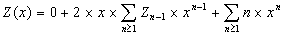
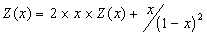
soit 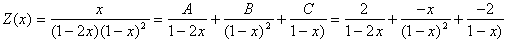
Nous avons donc 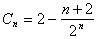
![]()
La complexité de l’organisation du tas en arbre est donc inférieure à 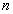
void trierTas( int t []){
organiserTas( t );
for( int i = t.length-1; i>=1; --i ){
echanger(t[0], t[i-1]);
descendre(t, 1, i-1);
}
}
2 éléments vont descendre au maximum de 1 place , 4 éléments vont descendre au maximum de 2 places, ... i éléments vont descendre au maximum de 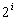 places. Supposons que m soit la première puissance de 2 supérieure ou égale à n.
places. Supposons que m soit la première puissance de 2 supérieure ou égale à n.
On obtient la récurrence suivante :
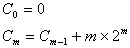
Resolvons la récurrence 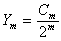
Soit 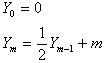
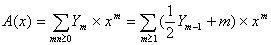
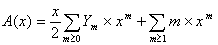
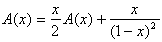
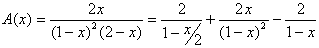
Donc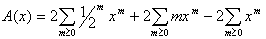
et 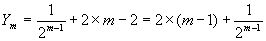
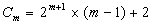 et donc
et donc