Précédent / Suivant / Table des matières
I-1. Modèle statistique
Les données sont constituées d’une famille de N valeurs y1, y2, … yN résultant de l’observation de la variable dépendante dans les différentes conditions expérimentales définies par le plan de l’expérience. On appelle protocole expérimental cette famille et on note y(e) l’observation de la VD dans la condition expérimentale e. L’élaboration du modèle qui décrit le processus de génération des données doit prendre en compte d’une part le fait que les mesures sont faites sur un échantillon aléatoire d’unités statistiques (fluctuations d’échantillonnage) et d’autre part qu’interviennent de façon aléatoire au cours de l’expérimentation des facteurs non contrôlés tels que par exemple les erreurs de mesure ou des facteurs individuels. L’observation y(e) est alors considérée comme la réalisation Y(e) d’une variable aléatoire Y. Le modèle du score décrit les effets des facteurs sur la variable aléatoire par le modèle algébrique : Y(e) = Z(e)+ε(e)
où :
· Z(e), appelé modèle structurel, décrit les effets des facteurs du plan
· ε(e), appelé résidu, mesure l’écart entre la variable réponse et le modèle structurel dû aux effets de facteurs non pris en compte dans le plan de l’expérience.
Ce modèle linéaire est caractérisé par des hypothèses portant sur le résidu
· ε(e) est une variable aléatoire de moyenne nulle.
· Var (ε(e))=σ2 pour tout e homoscédasticité ou homogénéité des variances des résidus
· Cor[(ε(e) , ε(e’)]=0 pour tout e≠e’ non corrélation des résidus
Ce modèle linéaire est aussi caractérisé par des
hypothèses portant sur le modèle structurel
Z(e) = μ(e)+A(e)
· μ(e) est une fonction déterministe de e qui décrit les effets des modalités des facteurs à effets fixes présentes dans e.
· A(e) est une variable aléatoire non corrélée avec ε(e), qui décrit les effets des facteurs à effets aléatoires
· ε(e) suit une loi normale N(0, σ2)
Selon la forme du modèle structurel, on distingue trois classes de modèles d’analyse de la variance :
ANOVA modèle 1 : Le modèle ne contient pas
de terme aléatoire A(e) : Y(e) = μ(e)+ε(e)
Ce modèle correspond à des plans où tous les facteurs sont à effets fixes.
Leurs effets portent uniquement sur la moyenne de la VD. Y(e) est
distribué selon une N(μ(e) , σ2).
ANOVA modèle 2 : (modèle des composantes
de la variance) Le terme déterministe est constant Y(e) = μ+A(e) +ε(e)
Ce modèle correspond à des plans où tous les facteurs sont à effets aléatoires.
Leurs effets portent sur la variance de la VD. Y(e) est distribué
selon une N(μ , σ2+σ2A(e)).
ANOVA modèle 3 : (modèle mixte) c’est le modèle qui mélange les deux cas précédents
Ce modèle correspond à des plans où sont présents des facteurs à effets fixes et des facteurs à effets aléatoires. Y(e) est distribué selon une N(μ(e), σ2+σ2A(e)).
I-2. Décomposition de la variance associée à un facteur : (rappel)
Dans toute la suite Y désigne la variable dépendante et G un facteur à r modalités. Les N observations sont réparties en r classes g1, g2, … gr contenant respectivement n1, n2, … nr observations. (On a donc N = n1 + n2, + … + nr). Notons ys(i) l’observation associée au sujet s dans la classe gi
|
|
Facteur G (groupe) |
|
||||||||
|
Sujets |
g1 |
g2 |
… |
gi |
… |
gr |
|
|
|||
|
1 2 … s … … …
|
…
…
|
…
…
… |
… … … … … … … |
…
…
|
… … … … … … … |
…
…
… |
|
|
|||
|
Effectif |
n1 |
n2 |
… |
ni |
… |
nr |
|
|
|||
|
Total |
T1 |
T2 |
… |
Ti |
… |
Tr |
|
|
|||
|
Moyenne |
|
|
… |
|
… |
|
|
|
|||
Les observations de la variable dépendante Y peuvent différer sous l’effet de deux sources de variations :
· La variation à l’intérieur des classes (ou dans les classes) : variation intra
· La variation entre les classes : variation inter.
Le facteur étant constant à l’intérieur des classes, seule la variation inter peut être imputée à l’effet du facteur.
La variation intra est une variation individuelle correspondant à la variation des observations dans une même classe.
La variation inter est une variation systématique correspondant à la variation des classes. Elle exprime l’effet (éventuel) du facteur (VI).
La variation des observations sera mesurée en termes de dispersion autour de la moyenne à l’aide de la variance (ou de la somme des carrées des écarts à la moyenne).
La moyenne générale
des observations est donnée par :
La variation Totale des observations est mesurée
par la Somme des Carrés des écarts entre chacune des N observations et la moyenne générale :
En notant la moyenne des observations de la classe gi on a :
La variation à l’Intérieur de la classe gi est mesurée par la Somme des Carrés des écarts entre chaque observation de la classe et la
moyenne de cette classe :
La variation à l’intérieur
des classes est définie par la somme, pour toutes les classes, des sommes des
carrés intra :
Pour calculer la
variation-inter on se place dans le cas de la situation fictive où toutes les
observations d’une même classe sont égales à la moyenne de cette classe et on calcule la Somme des Carrés Inter :
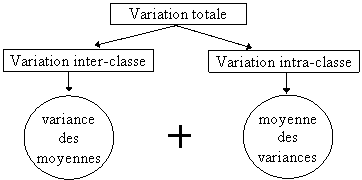
On démontre la relation fondamentale suivante : SCT = SCInter + SCIntra
Remarque : En divisant par l’effectif total N on a une relation analogue entre les variances :
Variance totale = Var Inter + Var Intra
Remarque : On retrouve l’indice de liaison PRE, appelé rapport de
corrélation (cf. cours de L1) en considérant le rapport :
mesure la liaison entre la variable réponse Y et le facteur G :
·
indique une absence de liaison (la réponse du
sujet ne dépend pas du groupe auquel il appartient).
·
indique une liaison parfaite (la réponse du
sujet est entièrement déterminée par son appartenance à un groupe).
Ainsi mesure l’intensité de l’effet de G sur la
réponse Y.
I-3. Distribution de Fisher-Snedecor
Proposition : Soient U1,
U2, …, Um , V1, V2,
…, Vn m+n
variables aléatoires indépendantes de même loi N(0, σ2) alors les variables sont indépendantes et de loi respective
Théorème : Soient U1,
U2, …, Um , V1, V2,
…, Vn m+n
variables aléatoires indépendantes de même loi N(0, σ2) alors la variable suit une loi de Fisher-Snedecor
F(m, n) de (m, n) degrés de liberté.
Remarque : Si F est une variable aléatoire de loi F(m, n) alors la variable aléatoire 1/F suit une loi F(n, m).
Corollaire : Soient U1,
U2, …, Um m variables aléatoires indépendantes de
même loi N(μ1, σ2) et V1, V2,
…, Vn n variables aléatoires indépendantes de même loi
N(μ2, σ2) indépendantes des Ui
alors la variable suit une loi de Fisher-Snedecor F(m-1, n-1).
Sont les estimateurs respectifs de μ1 et μ2
I-2-1 Exemple :
Pour étudier l’influence du facteur « intensité du bruit environnant » sur la capacité d’un sujet à résoudre un problème, l’expérimentateur construit l’expérience suivante : 24 écoliers sont répartis de façon aléatoire dans quatre pièces. Des bruits de la rue ont été enregistrés et sont diffusés dans chaque pièce avec un niveau sonore particulier. Les enfants doivent résoudre une série de problèmes. La variable réponse est la note finale obtenue à la série d’épreuves.
|
Niveau sonore |
|
|||
|
|
1 |
2 |
3 |
4 |
|
|
|
62 60 63 59
|
56 62 60 61 63 64 63 59 |
63 67 71 64 65 66
|
68 66 71 67 68 68
|
|
|
ni |
4 |
8 |
6 |
6 |
N = 24 |
|
|
61 |
61 |
66 |
68 |
|
|
Variance |
10/4 |
48/8 |
40/6 |
14/6 |
SCIntra= SCR = 112 |
|
|
36 |
72 |
24 |
96 |
SCInter=
|
SCT = N×variance totale = 340 SCIntra = 228 SCInter= 112