Précédent / Suivant / Table des matières

 

II-1. G est un (seul) facteur à effets fixes

II-1-1 Généralités

G est un facteur à r modalités (groupes) g₁, g₂, … g_r d’effectifs respectifs n₁, n₂, … n_r . N=n₁+n₂+ … +n_r. Y est la variable dépendante et ys(i) est le score du sujet s dans le groupe g_i (c’est l’observation associée au sujet s dans la modalité g_i).

 

 

On veut étudier l’effet du facteur G sur la variable réponse Y.

Pour cela on testera l’hypothèse nulle :         H₀ : le facteur n’a pas d’effet sur Y
contre l’hypothèse alternative :                      H₁ : le facteur a de l’effet sur Y.

 

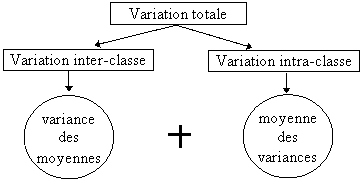
II-1-2 Décomposition de la variance (Rappel)

 

 

 

 

 

 

 

 

 

 

 

 

II-1-3 Modèle statistique (Modèle du score, modèle linéaire)

On veut étudier l’effet d’un facteur G à r modalités sur une variable réponse Y. On dispose pour chaque modalité i du facteur G de n_i observations. On note ys(i) l’observation du sujet s dans la modalité i.

ys(i) est la réalisation de la variable aléatoire Ys(i) décrite par le modèle suivant : Ys(i) = μ+α_i+εs(i)

où :

·     μ s’interprète comme un niveau général.

·     α_i mesure l’effet de la i^ème modalité du facteur G.

·     les variables aléatoires εs(i) sont indépendantes et de même loi N(0, σ²)

·     Pour tout i=1, 2,…, r. Les variances des r groupes sont homogènes (homoscédasticité)

·     On rajoute une contrainte d’identifiabilité:   (en moyenne les effets sont nuls)

On peut écrire l’hypothèse nulle et l’hypothèse alternative sous la forme suivante :

            hypothèse nulle           :           H₀ : α_i=0   pour tout i = 1, 2,…, r
            hypothèse alternative :            H₁ : l’un au moins des α_i est non nul

On montre alors les résultats suivants :

 

 

Remarque : Il est clair que les valeurs des variations (totale, inter et intra) dépendent des effectifs des modalités du facteur G. Aussi pour apprécier plus justement les grandeurs relatives à ces variations (en particulier pour comparer la variation due au facteur à la variation résiduelle), on calcule les carrés moyens des écarts, en divisant chaque variation par son nombre de degrés de liberté (ddl) :  

·     carrés moyens (total) : MCT
La variation totale concerne N scores (observations) ys(i) liés par une relation  donc présente N - 1 ddl et on a :  

·     carrés moyens inter : MCG
La variation inter(-groupes) concerne r groupes liés par une relation  donc présente r - 1 ddl et on a :  

·     carrés moyens intra (résiduels) : MCR
La variation intra (résiduelle) concerne N scores (observations) liés par r relations  donc présente N - r ddl et on a :  

Remarque : Tout comme les variations, les degrés de liberté sont additifs

 

Mais les carrés moyens ne sont pas additifs. En général MCT ≠ MCG + MCR.

 

 

Par conséquent : MCR est une estimation sans biais de la variance σ² et MCG est une estimation  de σ² augmentée d’un terme positif fonction des effets de groupe (  ).

Sous l’hypothèse nulle ( α_i = 0 pour tout i = 1,2,…,r)  MCG est aussi une estimation de σ².

 

 

 

 

Conclusion :

Le test d’hypothèse est alors défini au seuil de signification α par la règle de décision suivante :

Si F_obs ≥ λ_α  alors on rejette l’hypothèse nulle. λ_α étant donné par l’équation : α = P(F≥λ_α).

 

II-1-4 Tableau d’analyse de la variance

Les résultats sont souvent présentés sous forme d’un tableau :

 

Source de variation	Somme des carrés des écarts observés SCobs	ddl	Carrés moyens observés MCobs	F
G, Facteur, Inter-groupes, ...	SCG	r - 1	MCG
S<G>, Résiduelle, Intra	SCR	N - r	MCR	Flu = α =
Totale	SCT	N - 1

 

II-1-5 Exemple :

Pour étudier l’influence du facteur « intensité du bruit environnant » sur la capacité d’un sujet à résoudre un problème, l’expérimentateur construit l’expérience suivante : 24 écoliers sont répartis de façon aléatoire dans quatre pièces. Des bruits de la rue ont été enregistrés et sont diffusés dans chaque pièce avec un niveau sonore particulier. Les enfants doivent résoudre une série de problèmes. La variable réponse est la note finale obtenue à la série d’épreuves.

 

 

SCT = N×variance totale = 340                         .

On peut présenter les résultats dans le tableau d'analyse de variance :

En prenant un niveau de signification α=0,05=5%, on peut lire la valeur de λ_α dans la table de Fischer à r-1 = 3 et N-r = 20 degrés de liberté : λ_α = F_{(3 ; 20 ; 0,95)} = 3,10. Donc, si F_obs, la valeur observée de la statistique de test, est supérieure ou égale à 3,10 on rejette H₀ et dans le cas contraire, on conserve l'hypothèse H₀.

Conclusion : Comme F_obs=13,5714 > λ_α=3,10, on rejette H₀ pour accepter H₁ ; C’est-à-dire qu’il y a effectivement un effet du bruit environnant sur la capacité de résolution des problèmes. On rejette H₀ même avec un α=0,01=1%.

 

II-2. G est un (seul) facteur à effets aléatoires

II-2-1 Modèle statistique

On choisit un échantillon de r modalités g₁, g₂, … g_r du facteur G. On dispose pour chaque modalité échantillonnée de n_i observations de la variable dépendante (N=n₁+n₂+ … +n_r). On note ys(i) l’observation du sujet s dans le groupe g_i. Chaque observation ys(i) est la réalisation d’une variable aléatoire Ys(i) décrite par le modèle : Ys(i) = μ + Γ_i + εs(i)

où :

            μ est une constante mesurant le niveau général de la réponse

            Γ_i est une variable aléatoire qui mesure l’effet aléatoire de G.

            εs(i) est une variable aléatoire représentant le résidu.

 

On suppose réalisées les trois hypothèses suivantes :

·     les εs(i) sont des variables aléatoires indépendantes et de même loi N(0, σ²)

·     les Γ_i (i=1, 2, …, r) sont des variables aléatoires indépendantes de même loi N(0, σ_G²)

·     les Γ_i sont indépendantes des εs(i).

 

Le test d’hypothèse s’écrira alors :

            H₀ : G n’a pas d’effet  σ_G² = 0

            H₁ : G a un effet  σ_G² > 0

On montre alors les résultats suivants :

 

 

II-2-2 Test statistique

On se ramène donc au cas précédent et on utilisera la même statistique  pour réaliser le test.

 

II-2-3 Exemple :

On veut vérifier que l’intensité de traitement perceptif d’un visage dépend du visage examiné (certains visages retiennent plus l’attention que d’autres). Pour mettre à l’épreuve cette hypothèse de recherche, on construit l’expérience suivante :

 40 sujets sont choisis au hasard et répartis de façon aléatoire dans 5 groupes de 8 sujets chacun. Chaque groupe examine un visage choisi par l’expérimentateur au hasard dans l’ensemble de visages disponibles.

L’expérimentateur mesure l’intensité du traitement perceptif en observant la dilatation de la pupille lors de l’examen du visage. Il obtient les résultats suivants :

 

	Groupe des visages
Sujets	g1	g2	g3	g4	g5
1	58	60	63	64	57
2	51	61	55	64	59
3	57	66	57	65	65
4	59	65	60	61	63
5	56	59	61	66	62
6	54	59	62	59	64
7	53	64	58	67	60
8	52	63	56	60	63
ni	8	8	8	8	8	N=40
	55	62,125	59	63,25	61,625	= 60,2
s’²i	7,5	6,6094	7,5	7,4375	6,4844	s’²=15,81

 

SCT = N s' ² = 40 × 15,81 = 632,4

SCG = N  = N  = 40 × 8,7038 = 348,15

SCR = N  = 8 × [7,5+6,6094+7,5+7,4375+6,4844] = 8 × 35,5313 = 284,25

On vérifie que : SCR = SCT - SCG = 632,4 - 348,15 = 284,25.

On peut présenter les résultats dans le tableau d'analyse de variance :

 

En prenant un niveau de signification α=0,05=5%, on peut lire la valeur de λ_α dans la table de Fischer à r-1 = 4 et N-r = 35 degrés de liberté : λ_α = F_{(4 ; 35 ; 0,95)} = 2,64

Conclusion : Comme F_obs=10,717> λ_α=2,64, on rejette H₀ pour accepter H₁ ; C’est-à-dire qu’il y a effectivement un effet du facteur visage. (  )

Remarque : En prenant un niveau de signification α=0,01=1%, on peut lire la valeur de λ_α dans la table de Fischer à r-1 = 4 et N-r = 35 degrés de liberté : λ_α = F_{(4 ; 35 ; 0,99)} = 3,91 et on tire la même conclusion.