Précédent / Suivant / Table des matières
III-1. Plan S<A×B> avec A et B deux facteurs à effets fixes
III-1-1 Généralités
Un tel plan quasi-complet défini par le croisement de deux facteurs A et B, est aussi appelé plan factoriel complet d’ordre 2. Chaque condition est répliquée sur des sujets différents. Le facteur sujet est emboîté dans le croisement A×B. L’analyse diffère selon que l’emboîtement est équilibré ou non. Dans toute la suite on ne considère que le cas équilibré.
On se propose d’étudier l’effet de la présence simultanée d’un facteur A à r modalités et d’un facteur B à c modalités sur une variable réponse Y. Le plan étant équilibré, on dispose pour chaque croisement des modalités i du facteur A et j du facteur B de n observations. On note ys(i,j) l’observation du sujet s dans le croisement (i,j).
|
|
|
Facteur B |
|||||
|
|
|
b1 |
b2 |
… |
bj |
… |
Bc |
|
|
a1 |
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
A |
… |
|
|
|
|
|
|
|
|
ai |
|
|
|
y1(i,j), y2(i,j),……yn(i,j) |
|
|
|
|
… |
|
|
|
|
|
|
|
|
ar |
|
|
|
|
|
|
Remarque : dans le cas où n=1, l’interaction des facteurs A et B est confondue avec le facteur sujet, on ne peut donc séparer les effets d’interaction des effets résiduels et on ne peut tester leur existence. Un tel plan n’est justifié que lorsque l’on peut modifier a priori la forme de l’interaction entre les facteurs. Dans toute la suite nous développons le cas n > 1.
III-1-2 Analyse descriptive des effets (principaux et interaction) :
Considérons, pour chaque croisement (i,j) de la modalité i de A et de la modalité j de B la moyenne obtenue :
|
|
|
Facteur B |
|
|
|||||
|
|
|
b1 |
b2 |
… |
bj |
… |
Bc |
moyennes |
|
|
|
a1 |
|
|
… |
|
… |
|
|
|
|
|
a2 |
|
|
… |
|
… |
|
|
|
|
A |
… |
… |
… |
… |
… |
… |
… |
… |
|
|
|
ai |
|
|
… |
|
… |
|
|
|
|
|
… |
… |
… |
… |
… |
… |
… |
… |
|
|
|
ar |
|
|
… |
|
… |
|
|
|
|
|
moyennes |
|
|
… |
|
… |
|
|
|
La colonne marginale des moyennes par modalité de A (indépendamment de B) « traduit » l’effet principal du facteur A. De même la ligne marginale des moyennes par modalité de B (indépendamment de A) « traduit » l’effet principal du facteur B. Les différentes moyennes correspondant au croisement des modalités « traduisent » l’interaction des deux facteurs A et B.
III-1-3 Représentation géométrique des différents effets :
Les différentes combinaisons des effets principaux et d’interaction peuvent être illustrés par des graphiques dans lesquels on représente les moyennes en fonction des modalités de l’un des facteurs. Il y a deux graphiques possibles selon le facteur porté en abscisse.
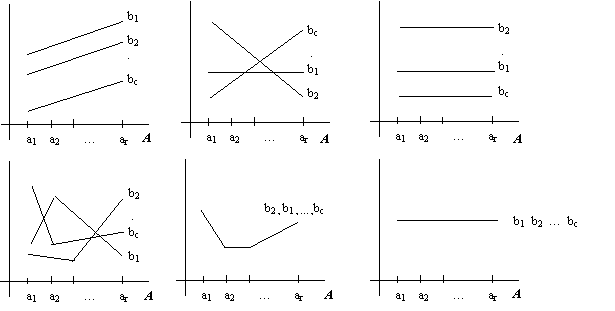
Le parallélisme des lignes traduit le fait que l’effet du facteur A (ou B) sur la variable réponse Y est le même quelque soit la valeur du facteur B (ou A). Les effets des facteurs A et B sont additifs et il n’y a pas d’effet de l’interaction entre les deux facteurs A et B sur Y.
Le non parallélisme des lignes traduit le fait que l’effet du facteur A (ou du facteur B) n’est pas le même en fonction de la modalité du facteur B (ou du facteur A). Les effets des facteurs A et B sur la variable Y ne sont pas additifs. Aux effets simples des facteurs s’ajoutent l’effet de l’interaction entre les deux facteurs.
Le parallélisme avec l’axe des abscisses traduit l’absence d’effet du facteur A (ou B). De plus si les différentes lignes correspondant aux modalités de B (ou A) sont confondues c’est l’absence totale d’effets.
III-1-4 Le modèle :
Rappelons que l’on veut étudier l’effet de la présence simultanée d’un facteur A à r modalités et d’un facteur B à c modalités sur une variable réponse Y. Le plan étant équilibré, on dispose pour chaque modalité i du facteur A et pour chaque modalité j du facteur B de n observations (n > 1). On note ys(i,j) l’observation du sujet s dans le croisement (i,j). ys(i,j) est la réalisation de la variable aléatoire Ys(i,j) décrite par le modèle suivant :
Ys(i,j) = μij + εs(i,j)
où les variables aléatoires εs(i,j) sont indépendantes et de même loi N(0,σ2) et
μij = μ + αi + βj + (αβ)ij où
- μ mesure la moyenne de la population
- les αi mesurent les effets principaux du facteur A
- les βj mesurent les effets principaux du facteur B
- les (αβ)ij mesurent les effets d’interaction.
On rajoute (comme hypothèses) les contraintes d’identifiabilité suivantes :
III-1-5 Décomposition de la variation :
A partir du tableau des données on calcule les Sommes des Carrés associées aux différentes sources de variation. Le croisement des facteurs A et B permet de décomposer la variation totale en somme de deux variations :
SCTobs = SCIintercase + SCIintracase = SC(A×B)obs + SCRobs
avec :
D’autre part le facteur élémentaire A (resp B) définit une partition de l’ensemble des observations en classes à laquelle correspond une somme de carrés observée mesurant la variation associée à l’effet principal de A (resp de B) :
Définition : On appelle somme des carrés associée à l’interaction la quantité :
SCABobs = SC(A×B)obs - SCAobs - SCBobs
On montre que :
Dans le cadre du modèle statistique ces sommes de carrés sont des réalisations de variables aléatoires dont on calcule les espérances et plus généralement les distributions des probabilités.
On montre le théorème fondamental suivant :
Théorème : Sous les hypothèses du modèle, les statistiques SCA, SCB, SCAB et SCR sont indépendantes et d’espérances respectives :
On ramène toutes les sommes
de carrés à des moyennes de carrés en divisant par les degrés de liberté
correspondant.
Ceci permet de réécrire le théorème précédent pour les moyennes des carrés :
Théorème : Sous les hypothèses du modèle, les statistiques MCA, MCB, MCAB et MCR sont indépendantes et d’espérances respectives :
III-1-6 Tests et décisions statistiques :
Le théorème précédent nous permet de tester l’existence des différents effets des facteurs. On peut construire des tests indépendants sur chacune des sources de variations :
Test 1 :
hypothèse nulle H0A : pas d’effet
principal du facteur A (
i) αi = 0 contre
l’hypothèse alternative : H1A : il existe
un effet principal du facteur A (
i) αi ≠ 0
Test 2 :
hypothèse nulle H0B : pas d’effet
principal du facteur B (
j) βj = 0 contre
l’hypothèse alternative : H1B : il existe
un effet principal du facteur B (
j) βj ≠ 0
Test 3 :
hypothèse nulle H0AB : pas d’effet
d’interaction (
i,j) (αβ)ij =
0 contre
l’hypothèse alternative : H1AB : il existe
une interaction (
i,j) (αβ)ij ≠ 0
La construction de ces tests résulte des trois corollaires du théorème suivant :
Théorème :
Dans le cadre du modèle statistique, la statistique SCR/σ2
suit une loi de χ2 à rc(n
- 1) degrés de liberté, sous l’hypothèse nulle H0A la statistique SCA/σ2
suit une loi de χ2 à r - 1 degrés de liberté, sous
l’hypothèse nulle H0B
la statistique SCB/σ2 suit une loi de χ2 à c - 1 degrés de liberté, sous l’hypothèse nulle H0AB la
statistique SCAB/σ2 suit une loi de χ2 à (r - 1)(c - 1) degrés de
liberté et ces statistiques sont indépendantes.
Corollaire : sous l’hypothèse H0A,
la statistique suit une loi de Fischer à
r - 1 et rc(n - 1) degrés de liberté.
Le test1 est alors défini au seuil de signification α par la règle de décision suivante :
si FA obs ≥ λα alors on rejette l’hypothèse nulle
où λα est donné par l’équation : α = P(FA ≥ λα).
Corollaire : sous l’hypothèse H0B,
la statistique suit une loi de Fischer à
c - 1 et rc(n - 1) degrés de liberté.
Le test2 est alors défini au seuil de signification α par la règle de décision suivante :
si FB obs ≥ λα alors on rejette l’hypothèse nulle
où λα est donné par l’équation : α = P(FB ≥ λα).
Corollaire : sous l’hypothèse H0AB,
la statistique suit une loi de Fischer à
(r
- 1)(c - 1) et rc(n
- 1) degrés de liberté.
Le test3 est alors défini au seuil de signification α par la règle de décision suivante :
si FAB obs ≥ λα alors on rejette l’hypothèse nulle
où λα est donné par l’équation : α = P(FAB ≥ λα).
On présente l’étude dans le :
tableau d’analyse de la variance :
|
Source |
SCobs |
ddl |
MCobs |
Fobs |
|
A |
SCAobs |
r - 1 |
MCAobs |
FA obs |
|
B |
SCBobs |
c - 1 |
MCBobs |
FB obs |
|
AB |
SCABobs |
(r - 1)(c - 1) |
MCABobs |
FAB obs |
|
R |
SCRobs |
rc(n - 1) |
MCRobs |
|
|
Total |
SCTobs |
rcn - 1 |
|
|
Pratique des calculs :
Calcul de SCA :
= ncr×variance des moyennes de A
Calcul de SCB :
= ncr×variance des moyennes de B
Calcul de SC(A×B) :
= ncr×variance des moyennes des carrés croisés
Calcul de SC(AB) :
SC(AB)obs = SC(A×B)obs - SCAobs - SCBobs
Calcul de SCT :
SCTobs = ncr×variance de toutes les données
Calcul de SCR :
SCRobs = SCTobs - SC(A×B)obs= SCTobs - SC(AB)obs- SCAobs - SCBobs
III-1-7 Exemple :
Un expérimentateur veut mettre à l’épreuve l’hypothèse que le niveau d’excitation physiologique d’une personne frustrée dépend du type d’agression autorisée. Il construit alors l’expérience suivante : 30 sujets choisis au hasard sont répartis de façon aléatoire en 6 groupes de 5 sujets, correspondant aux 6 conditions expérimentales définis par le croisement de deux facteurs
|
|
A1 |
A2 |
|
B1 |
1 6 4 3 0 |
8 8 10 8 11 |
|
B2 |
3 5 2 4 4 |
6 8 4 4 3 |
|
B3 |
6 7 4 5 3 |
5 7 3 -1 1 |
A : Facteur frustration :
2 modalités : A1 : frustré A2 : non frustré
B : Facteur agression :
3 modalités : B1 : non agressif B2 : moyennement agressif B3 : très agressif
Les résultats sont donnés par le tableau ci-contre.
|
|
A1 |
A2 |
Moyenne |
|
B1 |
|
|
|
|
B2 |
|
|
|
|
B3 |
|
|
|
|
Moyenne |
|
|
|
Calcul de SCA :
= ncr×variance
des moyennes de A
SCAobs = 30×1,0 = 30,0
Calcul de SCB :
= ncr×variance des moyennes de B SCBobs
= 30×0,6067
= 18,2
Calcul de SC(A×B) :
= ncr×variance des moyennes des carrés croisés
SC(A×B)obs= 30×4,1867 = 125,6
Calcul de SC(AB) :
SC(AB)obs = SC(A×B)obs - SCAobs - SCBobs = 125,6 - 30,0 - 18,2 = 77,4
Calcul de SCT :
SCTobs = ncr×variance de toutes les données SCTobs = 30×7,16 = 214,8
Calcul de SCR :
SCRobs = SCTobs - SC(A×B)obs = 214,8 - 125,6 = 89,2
On présente l’étude dans le :
tableau d’analyse de la variance :
|
Source |
SCobs |
ddl |
MCobs |
Fobs |
|
A |
SCAobs= 30,0 |
r - 1= 1 |
MCAobs= 30,0 |
FA obs= 8,0717 |
|
B |
SCBobs= 18,2 |
c - 1= 2 |
MCBobs= 9,1 |
FB obs= 2,4484 |
|
AB |
SCABobs= 77,4 |
(r - 1)(c - 1) = 2 |
MCABobs= 38,7 |
FAB obs= 10,4126 |
|
R |
SCRobs= 89,2 |
rc(n - 1) = 24 |
MCRobs= 3,7167 |
|
|
Total |
SCTobs= 214,8 |
rcn - 1= 29 |
|
|