Analyse du plan SXO

Précédent / Suivant / Table des matières

Chapitre IV

Analyse du plan S×0

El Methni M.

IV-1. O est un (seul) facteur à effets fixes

IV-1-1 Généralités

O est un facteur à r modalités o₁, o₂, … o_r (Occasions). S est le facteur sujet (à effets aléatoires) dont les modalités sont les n sujets s₁, s₂, … s_n. Pour chaque modalité du facteur O on « utilise » les n sujets. On a donc des mesures y_sirépétées pour chaque sujet s dans l’occasion (modalité) O_i.

En psychologie et en méthodologie on parle de plan intra, en statistique on parle de plan à mesures répétées.

On dispose donc de N=n×r mesures y_si que l’on présente sous la forme d’un tableau :

	Facteur O (Occasions)
Sujets	o₁	o₂	…	o_i	…	o_r
s₁	y₁₁	y₁₂	…	y_1i	…	y_1r
s₂	y₂₁	y₂₂	…	y_2i	…	y_2r
…	…	…	…		…	…
s_s	y_s₁	y_s₂	…	y_si	…	y_sr
…	…	…	…	…	…	…
s_n	y_n₁	y_n₂		y_ni		y_nr

Remarque : Un premier avantage d’un tel plan par rapport au plan S<O> est une « économie » du nombre de sujets. D’autre part avec un tel plan on peut diminuer l’erreur expérimentale (résidu). En effet le contrôle du facteur sujet permet de séparer son effet des effets résiduels. Mais le résidu sera confondu avec l’interaction entre S et O.

IV-1-2 Modèle univarié :

Les données peuvent être d’une part, considérées comme les N=n×r observations de la variable réponse Y dans les N=n×r conditions expérimentales décrites par le croisement du facteur sujet et du facteur occasion. Elles peuvent d’autre part, être regardées comme les n observations d’un vecteur de r variables réponses. Ces deux points de vue conduisent à l’élaboration de deux modèles, le modèle mixte univarié dans le premier cas et le modèle multivarié dans le second (voir condition de validation IV-1-5).

Nous étudierons le modèle mixte univarié dans lequel on considère que les modalités du facteur sujet ont été obtenues par échantillonnage, le facteur sujet est donc un facteur aléatoire. Le facteur occasion est lui un facteur à effets fixes.

Chaque donnée y_si correspond alors à l’observation d’une variable aléatoire réelle Y_si décrite par le modèle suivant : Y_si = μ_i + π_s + ε_si

Où :

· les μ_i sont des constantes mesurant les effets fixes des modalités i (i=1, 2, …, r) du facteur O

· les π_s sont des variables aléatoires indépendantes de loi N(0, σ²_π) mesurant les effets aléatoires des modalités s (s=1, 2, …, n) du facteur S

· les résidus ε_si sont des variables aléatoires indépendantes de loi N(0, σ²). On suppose en plus que les π_s et les ε_si sont indépendantes.

On peut réécrire l’effet de la modalité i sous la forme : μ_i = μ + α_i on a donc : Y_si = μ + α_i + π_s + ε_si

Où :

· μ constante s’interprétant comme un niveau général de réponse

· les α_i sont des constantes mesurant les effets fixes des modalités i et vérifiant : (contrainte d’identifiabilité)

Conséquence : D’après ce modèle les Y_si sont des variables aléatoires de loi N(μ+α_i, σ²_π+σ²). L’effet du facteur fixe se traduit sur la moyenne de la variable réponse tandis que l’effet du facteur aléatoire se traduit sur la variance de la variable réponse.

Pour ce modèle, l’interaction entre le facteur sujet et le facteur occasion est confondue avec le résidu car pour chaque modalité de l’un et de l’autre on ne dispose que d’une seule observation.

IV-1-3 Décomposition de la variation :

On décompose la variation totale en variation inter-sujets (due au facteur sujet) et variation intra-sujets (due à l’effet du facteur O). SCT_obs= SC_inter-sujets+ SC_intra-sujets

La variation inter-sujets est due au facteur sujet et la variation intra-sujets est due d’une part à l’effet du facteur O et d’autre part à l’effet des autres facteurs non contrôlés

SC_intra-sujets = SCO_obs+ SCR_obs

Conclusion : Dans le cas du plan complet S×O, la variation totale se décompose de façon additive en : SCT_obs= SCS_obs+ SCO_obs+ SCR_obs

De même on a la décomposition des degrés de liberté : nr-1 = (n-1) + (r-1) + (n-1)(r-1)

Les différentes sommes de carrées se calculent par :

SCR est calculé par : SCR_obs= SCT_obs - SCS_obs- SCO_obs

En pratique on peut effectuer les calculs en utilisant le tableau suivant :

	Facteur O (Occasions)
Sujets	o₁	o₂	…	o_i	…	o_r
s₁	y₁₁	y₁₂	…	y_1i	…	y_1r
s₂	y₂₁	y₂₂	…	y_2i	…	y_2r
…	…	…	…		…	…	…	…
s_s	y_s₁	y_s₂	…	y_si	…	y_sr
…	…	…	…	…	…	…	…	…
s_n	y_n₁	y_n₂		y_ni		y_nr
			…		…

IV-1-4 Statistiques des tests :

On montre le théorème suivant :

Théorème : sous les hypothèses du modèle on a

· E(SCO) = (r - 1)σ² + ∑nα_i²

· E(SCS) = (n - 1)(σ² + rσ²_π)

· E(SCR) = (n - 1)(r - 1)σ²

En considérant les moyennes des carrés :

On peut réécrire le théorème précédent sous la forme :

Théorème : sous les hypothèses du modèle on a

· E(MCR) = σ²

De nouveau on constate que MCR est un estimateur sans biais de la variance σ² et que MCO est un également un estimateur de la variance σ² augmentée d’une valeur positive traduisant l’effet du facteur. On considérera donc la statistique pour effectuer le test suivant :

Test de l’effet du facteur O sur la variable Y :

hypothèse nulle H₀ : O n’a pas d’effet (i) α_i = 0 (tous les α_i sont nuls) contre l’hypothèse alternative : H₁ : O a un effet (i) α_i ≠ 0 (l’un au moins des α_i est non nul).

Sous l’hypothèse nulle MCO et MCR sont deux estimateurs indépendants de σ² , leur rapport F_O est distribué selon une loi de Fischer à ν₁ = r - 1 et ν₂ = (n - 1)(r - 1) ddl.

Le test est alors défini au seuil de signification α par la règle de décision suivante :

si F_O_obs ≥ λ_α alors on rejette l’hypothèse nulle

où λ_α est donné par l’équation : α = P(F_O≥λ_α).

Les résultats sont présentés dans le tableau d’analyse de la variance suivant :

Source de variation	SC	ddl	MC	F_O
Inter S	SCS_obs	n - 1	MCS_obs
Intra S	SC_intra-sujets	n(r 1)
O	SCO_obs	r - 1	MCO_obs	F_O_obs
R	SCR_obs	(n - 1)(r - 1)	MCR_obs
Total	SCT_obs	rn - 1 =N - 1

IV-1-5 Condition de validation :

Le fait de mesurer plusieurs fois la variable réponse sur le même sujet introduit des corrélations entre les observations faites sur ce même sujet. Dans le cas du modèle mixte univarié on montre que :

Dans le cas du modèle multivarié on considère que les données sont les réalisations de r vecteurs aléatoires de dimension n. Y_s=(Y_s₁, Y_s₂, …, Y_sr) indépendants et de même loi normale caractérisés par : E(Y_si)=μ_i Var(Y_si)=σ²_i cov(Y_si , Y_si_’) = cov_ii’

Le modèle mixte univarié est donc un cas particulier du modèle multivarié se caratérisant par un matrice de variance-covariance Σ de la forme :

Une telle matrice où tous les termes sont positifs et où tous les termes diagonaux sont égaux et tous les autres sont égaux est dite matrice circulaire, et cette propriété est appelée la symétrie composée de la matrice.

Sur la diagonale principale de la matrice des variances-covariances Σ se trouvent les variances et les éléments hors diagonale sont des covariances.

L’hypothèse d’homogénéité des variances (homoscédasticité) se traduit par l’égalité des éléments de la diagonale de la matrice Σ, Les éléments en dehors de la diagonale principale de la matrice Σ doivent être de même ordre.

De même on peut considérer la matrice des corrélations ρ :

De ce fait, dans le cas du choix de modèle mixte univarié, en calculant les variances-covariances nous obtenons l’estimation de la matrice des variances-covariances (et aussi l'estimation de la matrice des corrélations).

Si les éléments de la diagonale de la matrice des variances-covariances sont de même ordre, alors la condition de l'homoscédasticité (homogénéité des variances) est vérifiée.

Si les éléments hors diagonale de la matrice des variances-covariance (ou des corrélations) sont de même ordre que les variances, alors le choix du modèle mixte univarié est justifié. C'est-à-dire que la condition de la circularité (de sphéricité) est acquise.

IV-1-6 Exemple :

Pendant d’heure on compte le nombre d’actions exercées par chacun des 7 rats sur un levier. Et ceci dans trois conditions de renforcement :

1^ere condition : on présente au rat des aliments très appréciés.

2^eme condition : on présente au rat des aliments moyennement appréciés.

3^eme condition : on présente au rat des aliments peu appréciés.

On obtient les résultats donnés par le tableau ci-contre.

		Facteur	O
Sujets	A	B	C	moyenne
s₁	8	6	2	=5,333	1,416
s₂	6	5	1	=4	0,020
s₃	7	5	0	=4	0,020
s₄	9	3	3	=5	0,734
s₅	5	4	1	=3,333	0,656
s₆	7	5	2	=4,667	0,274
s₇	6	2	0	=2,667	2,178
moyenne	=6,857	=4,286	=1,286	=4,143	5,298×3=15,90
	7,365	0,020	8,162	15,547×7=108,857

SCT=138,5714 SCO=108,857

SCS=15,90 SCR=SCT- SCO- SCS=13,8

Les résultats sont présentés dans le tableau d’analyse de la variance suivant :

Source de variation	SC	ddl	MC	F_O
Inter S	SCS_obs=15,90	n 1=6	MCS_obs=2,65
Intra S	SC_intra-sujets	n(r 1)=14
O	SCO_obs=108,857	r 1=2	MCO_obs=54,45	F_O_obs=47,34
R	SCR_obs=13,8	(n - 1)(r - 1)=12	MCR_obs=1,15
Total	SCT_obs=138,5714	rn - 1 =N 1=20

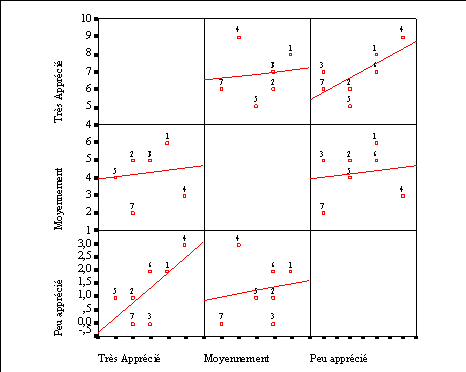
Pour vérifier la condition de la symétrie composée, nous allons établir la matrice des variances-covariances et aussi la matrice des corrélations pour les colonnes du tableau des observations.

Matrice des variances-covariances

Matrice des corrélations

On constate que les estimations des variances ne sont pas très différentes. L’hypothèse d’homogénéité des variances (homoscédasticité) peut être considérée comme acquise.

En ce qui concerne les covariances ou les corrélations, on constate une corrélation relativement forte entre les résultats des conditions 1 et 3 (r₁₃= 0,7).

Dans la condition 3 (aliments peu appréciés), les rats n'ont pas trop d'actions. Mais, les rats très actifs dans la condition 1 (aliments très appréciés) sont aussi actifs dans la condition 3, alors que les résultats de la condition 2 ne sont pas corrélés ni avec la condition 1 ni avec la condition 2.

Ces résultats suggèrent une réflexion supplémentaire sur ces données. Peut être faut-il examiner un modèle multivarié et effectuer une MANOVA.

El Methni M.

IV-1. O est un (seul) facteur à effets fixes

IV-1-1 Généralités

En psychologie et en méthodologie on parle de plan intra, en statistique on parle de plan à mesures répétées.

On dispose donc de N=n×r mesures y_si que l’on présente sous la forme d’un tableau :

	Facteur O (Occasions)
Sujets	o₁	o₂	…	o_i	…	o_r
s₁	y₁₁	y₁₂	…	y_1i	…	y_1r
s₂	y₂₁	y₂₂	…	y_2i	…	y_2r
…	…	…	…		…	…
s_s	y_s₁	y_s₂	…	y_si	…	y_sr
…	…	…	…	…	…	…
s_n	y_n₁	y_n₂		y_ni		y_nr

IV-1-2 Modèle univarié :

Chaque donnée y_si correspond alors à l’observation d’une variable aléatoire réelle Y_si décrite par le modèle suivant : Y_si = μ_i + π_s + ε_si

Où :

· les μ_i sont des constantes mesurant les effets fixes des modalités i (i=1, 2, …, r) du facteur O

· les π_s sont des variables aléatoires indépendantes de loi N(0, σ²_π) mesurant les effets aléatoires des modalités s (s=1, 2, …, n) du facteur S

· les résidus ε_si sont des variables aléatoires indépendantes de loi N(0, σ²). On suppose en plus que les π_s et les ε_si sont indépendantes.

On peut réécrire l’effet de la modalité i sous la forme : μ_i = μ + α_i on a donc : Y_si = μ + α_i + π_s + ε_si

Où :

· μ constante s’interprétant comme un niveau général de réponse

· les α_i sont des constantes mesurant les effets fixes des modalités i et vérifiant : (contrainte d’identifiabilité)

IV-1-3 Décomposition de la variation :

On décompose la variation totale en variation inter-sujets (due au facteur sujet) et variation intra-sujets (due à l’effet du facteur O). SCT_obs= SC_inter-sujets+ SC_intra-sujets

La variation inter-sujets est due au facteur sujet et la variation intra-sujets est due d’une part à l’effet du facteur O et d’autre part à l’effet des autres facteurs non contrôlés

SC_intra-sujets = SCO_obs+ SCR_obs

Conclusion : Dans le cas du plan complet S×O, la variation totale se décompose de façon additive en : SCT_obs= SCS_obs+ SCO_obs+ SCR_obs

De même on a la décomposition des degrés de liberté : nr-1 = (n-1) + (r-1) + (n-1)(r-1)

Les différentes sommes de carrées se calculent par :

SCR est calculé par : SCR_obs= SCT_obs - SCS_obs- SCO_obs

En pratique on peut effectuer les calculs en utilisant le tableau suivant :

	Facteur O (Occasions)
Sujets	o₁	o₂	…	o_i	…	o_r
s₁	y₁₁	y₁₂	…	y_1i	…	y_1r
s₂	y₂₁	y₂₂	…	y_2i	…	y_2r
…	…	…	…		…	…	…	…
s_s	y_s₁	y_s₂	…	y_si	…	y_sr
…	…	…	…	…	…	…	…	…
s_n	y_n₁	y_n₂		y_ni		y_nr
			…		…

IV-1-4 Statistiques des tests :

On montre le théorème suivant :

Théorème : sous les hypothèses du modèle on a

· E(SCO) = (r - 1)σ² + ∑nα_i²

· E(SCS) = (n - 1)(σ² + rσ²_π)

· E(SCR) = (n - 1)(r - 1)σ²

En considérant les moyennes des carrés :

On peut réécrire le théorème précédent sous la forme :

Théorème : sous les hypothèses du modèle on a

· E(MCR) = σ²

Test de l’effet du facteur O sur la variable Y :

hypothèse nulle H₀ : O n’a pas d’effet (i) α_i = 0 (tous les α_i sont nuls) contre l’hypothèse alternative : H₁ : O a un effet (i) α_i ≠ 0 (l’un au moins des α_i est non nul).

Sous l’hypothèse nulle MCO et MCR sont deux estimateurs indépendants de σ² , leur rapport F_O est distribué selon une loi de Fischer à ν₁ = r - 1 et ν₂ = (n - 1)(r - 1) ddl.

Le test est alors défini au seuil de signification α par la règle de décision suivante :

si F_O_obs ≥ λ_α alors on rejette l’hypothèse nulle

où λ_α est donné par l’équation : α = P(F_O≥λ_α).

Les résultats sont présentés dans le tableau d’analyse de la variance suivant :

Source de variation	SC	ddl	MC	F_O
Inter S	SCS_obs	n - 1	MCS_obs
Intra S	SC_intra-sujets	n(r 1)
O	SCO_obs	r - 1	MCO_obs	F_O_obs
R	SCR_obs	(n - 1)(r - 1)	MCR_obs
Total	SCT_obs	rn - 1 =N - 1

IV-1-5 Condition de validation :

Le modèle mixte univarié est donc un cas particulier du modèle multivarié se caratérisant par un matrice de variance-covariance Σ de la forme :

Sur la diagonale principale de la matrice des variances-covariances Σ se trouvent les variances et les éléments hors diagonale sont des covariances.

De même on peut considérer la matrice des corrélations ρ :

Si les éléments de la diagonale de la matrice des variances-covariances sont de même ordre, alors la condition de l'homoscédasticité (homogénéité des variances) est vérifiée.

IV-1-6 Exemple :

Pendant d’heure on compte le nombre d’actions exercées par chacun des 7 rats sur un levier. Et ceci dans trois conditions de renforcement :

1^ere condition : on présente au rat des aliments très appréciés.

2^eme condition : on présente au rat des aliments moyennement appréciés.

3^eme condition : on présente au rat des aliments peu appréciés.

On obtient les résultats donnés par le tableau ci-contre.

		Facteur	O
Sujets	A	B	C	moyenne
s₁	8	6	2	=5,333	1,416
s₂	6	5	1	=4	0,020
s₃	7	5	0	=4	0,020
s₄	9	3	3	=5	0,734
s₅	5	4	1	=3,333	0,656
s₆	7	5	2	=4,667	0,274
s₇	6	2	0	=2,667	2,178
moyenne	=6,857	=4,286	=1,286	=4,143	5,298×3=15,90
	7,365	0,020	8,162	15,547×7=108,857

SCT=138,5714 SCO=108,857

SCS=15,90 SCR=SCT- SCO- SCS=13,8

Les résultats sont présentés dans le tableau d’analyse de la variance suivant :

Source de variation	SC	ddl	MC	F_O
Inter S	SCS_obs=15,90	n 1=6	MCS_obs=2,65
Intra S	SC_intra-sujets	n(r 1)=14
O	SCO_obs=108,857	r 1=2	MCO_obs=54,45	F_O_obs=47,34
R	SCR_obs=13,8	(n - 1)(r - 1)=12	MCR_obs=1,15
Total	SCT_obs=138,5714	rn - 1 =N 1=20

Pour vérifier la condition de la symétrie composée, nous allons établir la matrice des variances-covariances et aussi la matrice des corrélations pour les colonnes du tableau des observations.

Matrice des variances-covariances

Matrice des corrélations

On constate que les estimations des variances ne sont pas très différentes. L’hypothèse d’homogénéité des variances (homoscédasticité) peut être considérée comme acquise.

En ce qui concerne les covariances ou les corrélations, on constate une corrélation relativement forte entre les résultats des conditions 1 et 3 (r₁₃= 0,7).

Ces résultats suggèrent une réflexion supplémentaire sur ces données. Peut être faut-il examiner un modèle multivarié et effectuer une MANOVA.