Précédent/ Suivant / Liste des thèmes
Travaux Dirigés N°3
Tableaux, diagrammes, mode, médiane, quartiles …
EL METHNI M.
EXERCICE I : (On reprend l’exercice I du TD2)
Afin d'établir un rapport éventuel entre l'âge et les loisirs un psychosociologue enquête auprès d'une population de 20 personnes et obtient les informations suivantes :
Notations S : Sport C : Cinéma T : Théâtre L : Lecture
|
Sujet |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
X: Age |
12 |
14 |
40 |
35 |
26 |
30 |
30 |
50 |
75 |
50 |
30 |
45 |
25 |
55 |
28 |
25 |
50 |
40 |
25 |
35 |
|
Y: Loisir |
S |
S |
C |
C |
S |
T |
T |
L |
L |
L |
T |
C |
C |
C |
S |
L |
L |
C |
T |
T |
|
S |
C |
T |
L |
|
12 |
|
|
|
|
14 |
|
|
|
|
26 |
|
|
|
|
28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1) Reprendre le tri à plat de
la variable Y réalisé au TD2 et
tracer un diagramme en bâtons le représentant. Proposer d’autres diagrammes
représentatifs. Peut-on parler de courbe cumulative ?
2) Donner les valeurs extrêmes ainsi
que le milieu de X. Cette question
a-t-elle un sens pour Y?
3) Déterminer le(s) mode(s) de Y. Comparer avec la représentation
graphique. Déterminer le(s) mode(s) de Y.
4) Calculer la médiane ainsi que les quartiles de X. Cette question a-t-elle un sens pour Y?
5) Dresser un tableau (à 2 dimensions) donnant la distribution de l’âge par type de loisir.
6) Calculer l’âge médian (la médiane des âges!) par type de loisir. Calculer la médiane de ces 4 médianes par type de loisir. Que conclure?
EXERCICE II :
Les dépenses d’aide sociale ont augmenté entre 1992 et 1994. Le journal « Le Monde » du 6 juillet 1995 nous le détaille sur un graphique donnant le pourcentage des augmentations par secteur accompagné d’un commentaire (à titre d’exemple) :
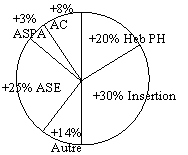
Pour
100 d’augmentation des dépenses nettes d’aide sociale
départementale :
-30 sont imputables à l’insertion,
-25 à l’aide sociale à l’enfance (ASE),
-20 à l’hébergement des personnes handicapées,
-8 à l’allocation compensatrice,
-3 à l’aide sociale aux personnes âgées,
-14 aux autres dépenses d’aide sociale.
Ces
informations encadrées sont justes et semblent cohérents avec le diagramme (on
a bien, par exemple, 30 parmi les 100
d’augmentation sont imputables à l’insertion
d’où le 30%). Mais à bien y réfléchir ce graphique est faux !
Pour vous aider à l’analyser et rectifier les erreurs : En cours on vous a
bien expliqué que les différents pourcentages totalisent 100%, ce qui est le
cas ici, et pourtant c’est là que réside le
« hic » ! ! !
Travail Personnel N°3
Sauf exception ces exercices ne seront pas traités en séances normales de travaux dirigés.
EXERCICE I : (On reprend l’exercice I du TP2)
Lors d'une enquête sur la publicité télévisée on a demandé à chaque sujet d’évaluer, en minutes, le temps des coupures publicitaires pendant le film du dimanche soir sur deux chaînes.
Les résultats obtenus sont récapitulés dans le tableau suivant :
|
Sujets |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
chaînes 1 |
35 |
29 |
30 |
31 |
33 |
32 |
33 |
34 |
32 |
33 |
32 |
30 |
28 |
34 |
33 |
33 |
|
chaînes 2 |
35 |
36 |
34 |
34 |
36 |
37 |
33 |
35 |
35 |
35 |
35 |
33 |
36 |
37 |
34 |
35 |
On désigne par X la variable : temps de coupure sur la chaînes 1 et par Y la variable : temps de coupure sur la chaînes 2.
1) Reprendre les tris à plat réalisés dans le TP2 et donner les représentations graphiques des distributions ainsi que celle des fonctions de répartition.
2) Donner les valeurs extrêmes ainsi que le milieu de X et de Y.
3) Calculer la médiane ainsi que les
quartiles de X et de Y.
4) On considère le tri à plat
relatif à X. (voir exercice I TP2
question 3).
|
xi |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
|
|
ni |
1 |
1 |
2 |
1 |
3 |
5 |
2 |
1 |
16 |
|
Ni |
1 |
2 |
4 |
5 |
8 |
13 |
15 |
16 |
|
a) Retrouver à partir de ce
tableau la médiane ainsi que les quartiles de X.
b)
Déterminer le(s) mode(s) de X.
Comparer avec la représentation graphique.
4) Reprendre la question (2) pour la
variable Y.
EXERCICE II :
On fait passer à 100 sujets une épreuve notée sur une échelle continue de 0 à 20. On obtient la distribution suivante :
0 0,5 1 1 1,5 2 2 2 3 3 4 4 4 4 4 4 4
4 4 4 4 4 4 4,5 4,5 4,5 4,5 4,5 4,5 4,5 5 5 5 5
5 5 5 5 5 5 5 5 5 5,5 5,5 6 6 6 6 6 6
6 6 6 6 6 6 6 6 6 6 6 6 6 6 6,5 6,5 6,5
6,5 6,5 6,5 6,5 6,5 6,5 6,5 6,5 6,5 6,5 6,5 6,5 7 7 7 7 7
7 7 7 7 7 8 8 8 8 8 8,5 8,5 8,5 9 10
1) Organiser cette
distribution en 5 classes de même amplitude. La borne inférieure de la 1ere
classe est 0 et la borne supérieure de la dernière classe est 10.
2) Dresser le tableau statistique
standard : (distribution des fréquences et des pourcentages, fréquences
cumulées et fonction de répartition, densité, centre des classes etc.)
3) Donner la représentation graphique
de la distribution ainsi que celle de la fonction de répartition.
4) Quelle est la classe de plus
grande densité? Comment l’appelle-t-on?
5) Pourquoi le calcul de la densité
est-il inutile dans ce cas ? Dans quel cas ce calcul est-il
nécessaire ?
6) Donner le(s) mode(s), les valeurs extrêmes et l’étendue de cette série statistique.
7) Calculer la médiane ainsi que les quartiles
8) On considère le tableau regroupant en 5 classes d’égales amplitudes les valeurs de X.
|
Note |
[0 2] |
]2 4] |
]4 6] |
]6 8] |
]8 10] |
|
|
ni |
8 |
15 |
42 |
30 |
5 |
100 |
|
Ni |
8 |
23 |
65 |
95 |
100 |
|
a)
Retrouver à partir de ce tableau la médiane ainsi que les quartiles de X. Comparer avec la question 2 et
commenter.
b)
Reporter ces valeurs sur la représentation graphique de la fonction de
répartition et commenter.
c)
Déterminer la(les) classe(s) modale(s). Comparer avec la représentation
graphique.
9) Calculer le 3ème et le
7ème décile. Que représente l’intervalle [d3 d7]?